Announcements¶
- The linear algebra and probability tutorial is next Monday's during lecture time in Kyra Gan's section
- The Python and Numpy tutorial is on Thursday of next week in class
- Homework 0 is out on Gradescope. It is optional, but useful to set up your environment for future homeworks.
Part 1: A Supervised Machine Learning Problem¶
Let’s start by revisting an example of supervised learning from the previous lecture.
Recall: Object Detection¶
An example of supervised learning is an object detection system.
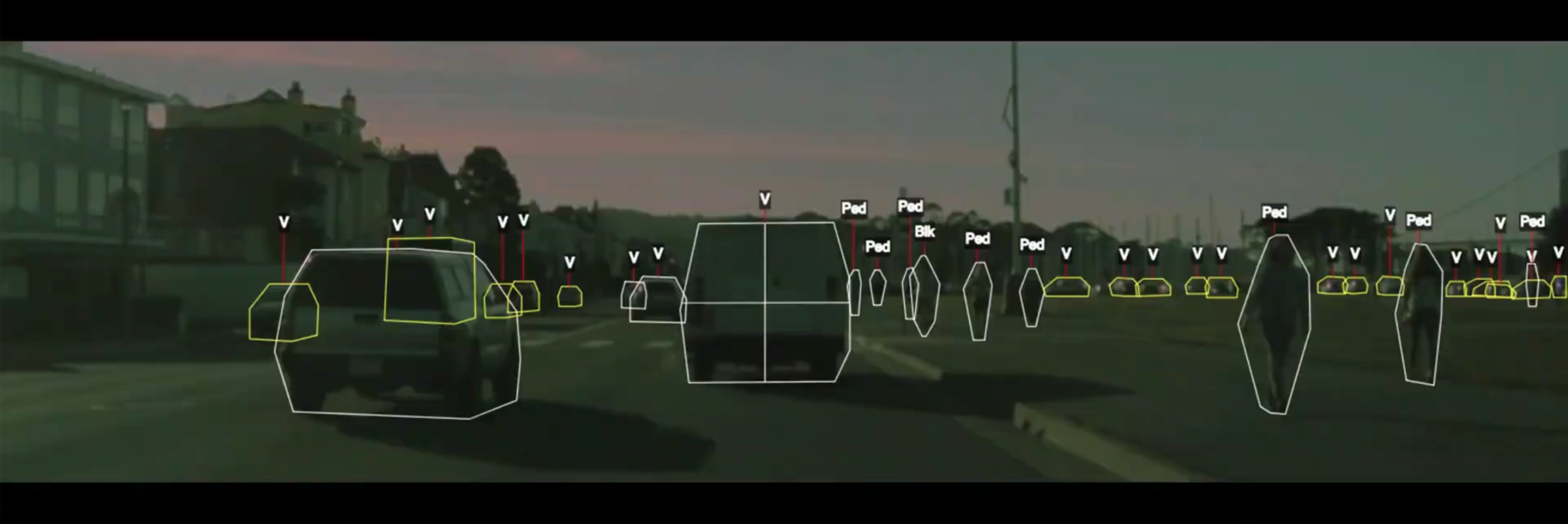
- First, we collect a dataset of labeled training examples.
- We train a model to output accurate predictions on this dataset.
- When the model sees new, similar data, it will also be accurate.
A Recipe for Applying Supervised Learning¶
To apply supervised learning, we define a dataset and a learning algorithm.
$$ \text{Dataset} + \text{Learning Algorithm} \to \text{Predictive Model} $$
The output is a predictive model that maps inputs to targets. For instance, it can predict targets on new inputs.
Why Supervised Learning?¶
Supervised learning can be useful in several ways.
- Making accurate predictions on new data. In many setting, there is no better way!
- Understanding the mechanisms through which input variables affect targets.
Applications of Supervised Learning¶
Many of the most important applications of machine learning are supervised:
- Classifying medical images.
- Translating between pairs of languages.
- Detecting objects in a self-driving car.
Part 2: Anatomy of a Supervised Learning Problem: The Dataset¶
We have seen an example of supervised machine learning.
Let's now examine more closely the components of a supervised learning problem, starting with the dataset.
A Supervised Learning Dataset¶
Let's dive deeper into what's a supervised learning dataset. We will use the UCI Diabetes Dataset as our example.
This dataset contains information about patients, including their age, sex, BMI, and blood pressure. We can ask sklearn to give us more information about this dataset.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [12, 4]
from sklearn import datasets
# Load the diabetes dataset
diabetes = datasets.load_diabetes(as_frame=True)
print(diabetes.DESCR)
.. _diabetes_dataset:
Diabetes dataset
----------------
Ten baseline variables, age, sex, body mass index, average blood
pressure, and six blood serum measurements were obtained for each of n =
442 diabetes patients, as well as the response of interest, a
quantitative measure of disease progression one year after baseline.
**Data Set Characteristics:**
:Number of Instances: 442
:Number of Attributes: First 10 columns are numeric predictive values
:Target: Column 11 is a quantitative measure of disease progression one year after baseline
:Attribute Information:
- age age in years
- sex
- bmi body mass index
- bp average blood pressure
- s1 tc, T-Cells (a type of white blood cells)
- s2 ldl, low-density lipoproteins
- s3 hdl, high-density lipoproteins
- s4 tch, thyroid stimulating hormone
- s5 ltg, lamotrigine
- s6 glu, blood sugar level
Note: Each of these 10 feature variables have been mean centered and scaled by the standard deviation times `n_samples` (i.e. the sum of squares of each column totals 1).
Source URL:
https://www4.stat.ncsu.edu/~boos/var.select/diabetes.html
For more information see:
Bradley Efron, Trevor Hastie, Iain Johnstone and Robert Tibshirani (2004) "Least Angle Regression," Annals of Statistics (with discussion), 407-499.
(https://web.stanford.edu/~hastie/Papers/LARS/LeastAngle_2002.pdf)
A Supervised Learning Dataset: Notation¶
We say that a training dataset of size $n$ (e.g., $n$ patients) is a set $$\mathcal{D} = \{(x^{(i)}, y^{(i)}) \mid i = 1,2,...,n\}$$
Each $x^{(i)}$ denotes an input (e.g., the measurements for patient $i$), and each $y^{(i)} \in \mathcal{Y}$ is a target (e.g., the diabetes risk).
Together, $(x^{(i)}, y^{(i)})$ form a training example.
We can look at the diabetes dataset in this form.
# Load the diabetes dataset
diabetes_X, diabetes_y = diabetes.data, diabetes.target
# Print part of the dataset
diabetes_X.head()
| age | sex | bmi | bp | s1 | s2 | s3 | s4 | s5 | s6 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.038076 | 0.050680 | 0.061696 | 0.021872 | -0.044223 | -0.034821 | -0.043401 | -0.002592 | 0.019908 | -0.017646 |
| 1 | -0.001882 | -0.044642 | -0.051474 | -0.026328 | -0.008449 | -0.019163 | 0.074412 | -0.039493 | -0.068330 | -0.092204 |
| 2 | 0.085299 | 0.050680 | 0.044451 | -0.005671 | -0.045599 | -0.034194 | -0.032356 | -0.002592 | 0.002864 | -0.025930 |
| 3 | -0.089063 | -0.044642 | -0.011595 | -0.036656 | 0.012191 | 0.024991 | -0.036038 | 0.034309 | 0.022692 | -0.009362 |
| 4 | 0.005383 | -0.044642 | -0.036385 | 0.021872 | 0.003935 | 0.015596 | 0.008142 | -0.002592 | -0.031991 | -0.046641 |
Training Dataset: Inputs¶
More precisely, an input $x^{(i)} \in \mathcal{X}$ is a $d$-dimensional vector of the form $$ x^{(i)} = \begin{bmatrix} x^{(i)}_1 \\ x^{(i)}_2 \\ \vdots \\ x^{(i)}_d \end{bmatrix}$$ For example, it could be the values of the $d$ features for patient $i$.
The set $\mathcal{X}$ is called the feature space. Often, we have, $\mathcal{X} = \mathbb{R}^d$.
Let's look at data for one patient.
diabetes_X.iloc[0]
age 0.038076 sex 0.050680 bmi 0.061696 bp 0.021872 s1 -0.044223 s2 -0.034821 s3 -0.043401 s4 -0.002592 s5 0.019908 s6 -0.017646 Name: 0, dtype: float64
Training Dataset: Attributes¶
We refer to the numerical variables describing the patient as attributes. Examples of attributes include:
- The age of a patient.
- The patient's gender.
- The patient's BMI.
Note that thes attributes in the above example have been mean-centered at zero and re-scaled to have a variance of one.
Training Dataset: Features¶
Often, an input object has many attributes, and we want to use these attributes to define more complex descriptions of the input.
- Is the patient old and a man? (Useful if old men are at risk).
- Is the BMI above the obesity threshold?
We call these custom attributes features.
Let's create an "old man" feature.
diabetes_X['old_man'] = (diabetes_X['sex'] > 0) & (diabetes_X['age'] > 0.05)
diabetes_X.head()
| age | sex | bmi | bp | s1 | s2 | s3 | s4 | s5 | s6 | old_man | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.038076 | 0.050680 | 0.061696 | 0.021872 | -0.044223 | -0.034821 | -0.043401 | -0.002592 | 0.019908 | -0.017646 | False |
| 1 | -0.001882 | -0.044642 | -0.051474 | -0.026328 | -0.008449 | -0.019163 | 0.074412 | -0.039493 | -0.068330 | -0.092204 | False |
| 2 | 0.085299 | 0.050680 | 0.044451 | -0.005671 | -0.045599 | -0.034194 | -0.032356 | -0.002592 | 0.002864 | -0.025930 | True |
| 3 | -0.089063 | -0.044642 | -0.011595 | -0.036656 | 0.012191 | 0.024991 | -0.036038 | 0.034309 | 0.022692 | -0.009362 | False |
| 4 | 0.005383 | -0.044642 | -0.036385 | 0.021872 | 0.003935 | 0.015596 | 0.008142 | -0.002592 | -0.031991 | -0.046641 | False |
Training Dataset: Features¶
We may denote features via a function $\phi : \mathcal{X} \to \mathbb{R}^p$ that takes an input $x^{(i)} \in \mathcal{X}$ and outputs a $p$-dimensional vector $$ \phi(x^{(i)}) = \left[\begin{array}{@{}c@{}} \phi(x^{(i)})_1 \\ \phi(x^{(i)})_2 \\ \vdots \\ \phi(x^{(i)})_p \end{array} \right]$$ We say that $\phi(x^{(i)})$ is a featurized input, and each $\phi(x^{(i)})_j$ is a feature.
Features vs Attributes¶
In practice, the terms attribute and features are often used interchangeably. Most authors refer to $x^{(i)}$ as a vector of features.
We will follow this convention and use the term "attribute" only when there is ambiguity between features and attributes.
Features: Discrete vs. Continuous¶
Features can be either discrete or continuous. We will see that some ML algorthims handle these differently.
The BMI feature that we have seen earlier is an example of a continuous feature.
We can visualize its distribution.
diabetes_X.loc[:, 'bmi'].hist()
<AxesSubplot:>
Other features take on one of a finite number of discrete values. The sex column is an example of a categorical feature.
In this example, the dataset has been pre-processed such that the two values happen to be 0.05068012 and -0.04464164.
print(diabetes_X.loc[:, 'sex'].unique())
diabetes_X.loc[:, 'sex'].hist()
[ 0.05068012 -0.04464164]
<AxesSubplot:>
Training Dataset: Targets¶
For each patient, we are interested in predicting a quantity of interest, the target. In our example, this is the patient's diabetes risk.
Formally, when $(x^{(i)}, y^{(i)})$ form a training example, each $y^{(i)} \in \mathcal{Y}$ is a target. We call $\mathcal{Y}$ the target space.
We plot the distirbution of risk scores below.
plt.xlabel('Diabetes risk score')
plt.ylabel('Number of patients')
diabetes_y.hist()
<AxesSubplot:xlabel='Diabetes risk score', ylabel='Number of patients'>
Targets: Regression vs. Classification¶
We distinguish between two broad types of supervised learning problems that differ in the form of the target variable.
- Regression: The target variable $y$ is continuous. We are fitting a curve in a high-dimensional feature space that approximates the shape of the dataset.
- Classification: The target variable $y$ is discrete. Each discrete value corresponds to a class and we are looking for a hyperplane that separates the different classes.
Part 3: Anatomy of a Supervised Learning Problem: The Learning Algorithm¶
Let's now look at what a general supervised learning algorithm looks like.
Recall: Three Components of a Supervised Machine Learning Problem¶
To apply supervised learning, we define a dataset and a learning algorithm.
$$ \text{Dataset} + \text{Learning Algorithm} \to \text{Predictive Model} $$
The output is a predictive model that maps inputs to targets. For instance, it can predict targets on new inputs.
The Components of a Supervised Machine Learning Algorithm¶
We can also define the high-level structure of a supervised learning algorithm as consisting of three components:
- A model class: the set of possible models we consider.
- An objective function, which defines how good a model is.
- An optimizer, which finds the best predictive model in the model class according to the objective function
Let's look again at our diabetes dataset for an example.
import numpy as np
import pandas as pd
from sklearn import datasets
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = [12, 4]
# Load the diabetes dataset
diabetes = datasets.load_diabetes(as_frame=True)
diabetes_X, diabetes_y = diabetes.data, diabetes.target
# Print part of the dataset
diabetes_X.head()
| age | sex | bmi | bp | s1 | s2 | s3 | s4 | s5 | s6 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.038076 | 0.050680 | 0.061696 | 0.021872 | -0.044223 | -0.034821 | -0.043401 | -0.002592 | 0.019908 | -0.017646 |
| 1 | -0.001882 | -0.044642 | -0.051474 | -0.026328 | -0.008449 | -0.019163 | 0.074412 | -0.039493 | -0.068330 | -0.092204 |
| 2 | 0.085299 | 0.050680 | 0.044451 | -0.005671 | -0.045599 | -0.034194 | -0.032356 | -0.002592 | 0.002864 | -0.025930 |
| 3 | -0.089063 | -0.044642 | -0.011595 | -0.036656 | 0.012191 | 0.024991 | -0.036038 | 0.034309 | 0.022692 | -0.009362 |
| 4 | 0.005383 | -0.044642 | -0.036385 | 0.021872 | 0.003935 | 0.015596 | 0.008142 | -0.002592 | -0.031991 | -0.046641 |
Model: Notation¶
We'll say that a model is a function $$ f : \mathcal{X} \to \mathcal{Y} $$ that maps inputs $x \in \mathcal{X}$ to targets $y \in \mathcal{Y}$.
Often, models have parameters $\theta \in \Theta$ living in a set $\Theta$. We will then write the model as $$ f_\theta : \mathcal{X} \to \mathcal{Y} $$ to denote that it's parametrized by $\theta$.
Model Class: Notation¶
Formally, the model class is a set $$\mathcal{M} \subseteq \{f \mid f : \mathcal{X} \to \mathcal{Y} \}$$ of possible models that map input features to targets.
When the models $f_\theta$ are paremetrized by parameters $\theta \in \Theta$ living in some set $\Theta$. Thus we can also write $$\mathcal{M} = \{f_\theta \mid \theta \in \Theta \}.$$
Model Class: Example¶
One simple approach is to assume that $x$ and $y$ are related by a linear model of the form \begin{align*} y & = \theta_0 + \theta_1 \cdot x_1 + \theta_2 \cdot x_2 + ... + \theta_d \cdot x_d \end{align*} where $x$ is a featurized input and $y$ is the target.
The $\theta_j$ are the parameters of the model, $\Theta = \mathbb{R}^{d+1}$, and $\mathcal{M} = \{ \theta_0 + \theta_1 \cdot x_1 + \theta_2 \cdot x_2 + ... + \theta_d \cdot x_d \mid \theta \in \mathbb{R}^{d+1} \}$
Objectives: Notation¶
To capture this intuition, we define an objective function (also called a loss function) $$J(f) : \mathcal{M} \to [0, \infty), $$ which describes the extent to which $f$ "fits" the data $\mathcal{D} = \{(x^{(i)}, y^{(i)}) \mid i = 1,2,...,n\}$.
When $f$ is parametrized by $\theta \in \Theta$, the objective becomes a function $J(\theta) : \Theta \to [0, \infty).$
Objective: Examples¶
What would are some possible objective functions? We will see many, but here are a few examples:
- Mean squared error: $$J(\theta) = \frac{1}{2n} \sum_{i=1}^n \left( f_\theta(x^{(i)}) - y^{(i)} \right)^2$$
- Absolute (L1) error: $$J(\theta) = \frac{1}{n} \sum_{i=1}^n \left| f_\theta(x^{(i)}) - y^{(i)} \right|$$
These are defined for a dataset $\mathcal{D} = \{(x^{(i)}, y^{(i)}) \mid i = 1,2,...,n\}$.
from sklearn.metrics import mean_squared_error, mean_absolute_error
y1 = np.array([1, 2, 3, 4])
y2 = np.array([-1, 1, 3, 5])
print('Mean squared error: %.2f' % mean_squared_error(y1, y2))
print('Mean absolute error: %.2f' % mean_absolute_error(y1, y2))
Mean squared error: 1.50 Mean absolute error: 1.00
Optimizer: Notation¶
At a high-level an optimizer takes an objective $J$ and a model class $\mathcal{M}$ and finds a model $f \in \mathcal{M}$ with the smallest value of the objective $J$.
\begin{align*} \min_{f \in \mathcal{M}} J(f) \end{align*}
Intuitively, this is the function that bests "fits" the data on the training dataset.
When $f$ is parametrized by $\theta \in \Theta$, the optimizer minimizes a function $J(\theta)$ over all $\theta \in \Theta$.
Optimizer: Example¶
We will see that behind the scenes, the sklearn.linear_models.LinearRegression algorithm optimizes the MSE loss.
\begin{align*} \min_{\theta \in \mathbb{R}} \frac{1}{2n} \sum_{i=1}^n \left( f_\theta(x^{(i)}) - y^{(i)} \right)^2 \end{align*}
We can easily measure the quality of the fit on the training set and the test set.
Let's run the above algorithm on our diabetes dataset.
# Collect 20 data points for training
diabetes_X_train = diabetes_X.iloc[-20:]
diabetes_y_train = diabetes_y.iloc[-20:]
# Create linear regression object
regr = linear_model.LinearRegression()
# Train the model using the training sets
regr.fit(diabetes_X_train, diabetes_y_train.values)
# Make predictions on the training set
diabetes_y_train_pred = regr.predict(diabetes_X_train)
# Collect 3 data points for testing
diabetes_X_test = diabetes_X.iloc[:3]
diabetes_y_test = diabetes_y.iloc[:3]
# generate predictions on the new patients
diabetes_y_test_pred = regr.predict(diabetes_X_test)
The algorithm returns a predictive model. We can visualize its predictions below.
# visualize the results
plt.xlabel('Body Mass Index (BMI)')
plt.ylabel('Diabetes Risk')
plt.scatter(diabetes_X_train.loc[:, ['bmi']], diabetes_y_train)
plt.scatter(diabetes_X_test.loc[:, ['bmi']], diabetes_y_test, color='red', marker='o')
# plt.scatter(diabetes_X_train.loc[:, ['bmi']], diabetes_y_train_pred, color='black', linewidth=1)
plt.plot(diabetes_X_test.loc[:, ['bmi']], diabetes_y_test_pred, 'x', color='red', mew=3, markersize=8)
plt.legend(['Model', 'Prediction', 'Initial patients', 'New patients'])
<matplotlib.legend.Legend at 0x12f6a46a0>
from sklearn.metrics import mean_squared_error
print('Training set mean squared error: %.2f'
% mean_squared_error(diabetes_y_train, diabetes_y_train_pred))
print('Test set mean squared error: %.2f'
% mean_squared_error(diabetes_y_test, diabetes_y_test_pred))
print('Test set mean squared error on random inputs: %.2f'
% mean_squared_error(diabetes_y_test, np.random.randn(*diabetes_y_test_pred.shape)))
Training set mean squared error: 1118.22 Test set mean squared error: 667.81 Test set mean squared error on random inputs: 15887.97
Summary: Components of a Supervised Machine Learning Problem¶
To apply supervised learning, we define a dataset and a learning algorithm.
$$ \underbrace{\text{Dataset}}_\text{Features, Attributes, Targets} + \underbrace{\text{Learning Algorithm}}_\text{Model Class + Objective + Optimizer } \to \text{Predictive Model} $$
The output is a predictive model that maps inputs to targets. For instance, it can predict targets on new inputs.
Notation: Feature Matrix¶
Suppose that we have a dataset of size $n$ (e.g., $n$ patients), indexed by $i=1,2,...,n$. Each $x^{(i)}$ is a vector of $d$ features.
Feature Matrix¶
Machine learning algorithms are most easily defined in the language of linear algebra. Therefore, it will be useful to represent the entire dataset as one matrix $X \in \mathbb{R}^{n \times d}$, of the form: $$ X = \begin{bmatrix} x^{(1)}_1 & x^{(2)}_1 & \ldots & x^{(n)}_1 \\ x^{(1)}_2 & x^{(2)}_2 & \ldots & x^{(n)}_2 \\ \vdots \\ x^{(1)}_d & x^{(2)}_d & \ldots & x^{(n)}_d \end{bmatrix}.$$
Similarly, we can vectorize the target variables into a vector $y \in \mathbb{R}^n$ of the form $$ y = \begin{bmatrix} y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(n)} \end{bmatrix}.$$