319. Bulb Switcher
There are n bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb.
On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the ith round, you toggle every i bulb. For the nth round, you only toggle the last bulb.
Return the number of bulbs that are on after n rounds.
Example 1:
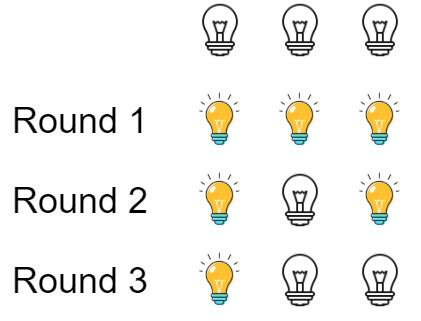
Input: n = 3 Output: 1 Explanation: At first, the three bulbs are [off, off, off]. After the first round, the three bulbs are [on, on, on]. After the second round, the three bulbs are [on, off, on]. After the third round, the three bulbs are [on, off, off]. So you should return 1 because there is only one bulb is on.
Example 2:
Input: n = 0 Output: 0
Example 3:
Input: n = 1 Output: 1
Constraints:
0 <= n <= 109
代码
class Solution {
public int bulbSwitch(int n) {
return (int) Math.sqrt(n);
}
}
// class Solution {
// public int bulbSwitch(int n) {
// boolean[] bulbs = new boolean[n + 1];
// for(int i = 1; i <= n; i++){
// for(int j = 1; j <= n; j++){
// if(j % i == 0){
// bulbs[j] = bulbs[j] == true ? false : true;
// }
// }
// }
// int count = 0;
// for(int j = 1; j <= n; j++){
// if(bulbs[j] == true){
// count += 1;
// }
// }
// return count;
// }
// }
思路
Approach 1: Math
Intuition
The idea behind this problem is to find the number of bulbs that are on after n rounds. In each round, we toggle some of the bulbs.
As all the bulbs are initially off, at the end only bulbs that are toggled an odd number of times will remain on.
Now, whenever we are at a round i we know we toggle all bulbs having a factor i. Thus, we need to find the bulbs which have an odd number of factors, as those bulbs will be toggled an odd number of times (once by each factor).
It might be unintuitive, but with a few examples, we can easily see that a perfect square number has an odd number of factors, since any number's factors come in pairs of two different numbers, but the square root of the number will be paired with itself.
Let's take an example to make it more clear. Suppose n = 10.
So, the number of rounds is 10. In each round, we will toggle some of the bulbs.
Track of rounds in which each bulb is toggled:
- Bulb 1: Round 1 (odd number of toggles)
- Bulb 2: Round 1, Round 2
- Bulb 3: Round 1, Round 3
- Bulb 4: Round 1, Round 2, Round 4 (odd number of toggles)
- Bulb 5: Round 1, Round 5
- Bulb 6: Round 1, Round 2, Round 3, Round 6
- Bulb 7: Round 1, Round 7
- Bulb 8: Round 1, Round 2, Round 4, Round 8
- Bulb 9: Round 1, Round 3, Round 9 (odd number of toggles)
- Bulb 10: Round 1, Round 2, Round 5, Round10
So, the number of bulbs that are on after 10 rounds is 3: Bulb 1, Bulb 4, and Bulb 9.
Now let's discuss, why do perfect squares have odd and non-perfect squares have an even number of factors?
A factor is a number that can be multiplied by another number to produce a given result. Say for 12, 1, 2, 3, 4, 6, 12 all are its factors as any factor x can be paired with another factor 12 / x and when multiplied together it will result in 12.
When we factorize a number y, say we have one factor x, then the other factor whose multiplication will result in the original number will be y / x.
Now comparing x and y / x, if y is a perfect square it means y = a * a, thus, here it is a possibility that x and y / x are same numbers, i.e. a.
But if y is not a perfect square then for each x we will have a unique y / x, thus, it's factor pairs will always exist as two different numbers (e.g: for 12 -> 1 x 12, 2 x 6, 3 x 4, (it has three factor pairs, so total 6 factors)), thus the total count of number of factors for non-perfect squares will be even,
and for perfect square, all other x and y / x factor pairs will be two different numbers except for one case, i.e. a and a (e.g: for 16 -> 1 x 16, 2 x 8, 4 x 4 (4 is paired with itself, it has three factor pairs, but one pair has both numbers same, so total 5 factors)). Thus, it will have odd number of total factors.
Thus we just need to find how many numbers from 1 to n are perfect squares.
We can iterate on each number and check if it's a perfect square or not, (i.e. floor(sqrt(i)) * floor(sqrt(i)) == i)
Or, we can directly find the square root of n and its floor value will be equal to the count of numbers whose squares exist in this range 1 to n.
The floor of the square root of n gives us the largest number whose square is less than or equal to n. For example, if n = 26, then the floor of square root of n is 5, which means the largest number whose square is less than or equal to 26 is 5 thus for each number from 1 to 5, its respective square will be present in the original range. So, there are 5 perfect squares in the range 1 to 25 (1, 4, 9, 16, and 25).
So, taking the floor value of the square root of n will give us the number of perfect squares in the range 1 to n.
Hence, sqrt(n) is our answer to this problem.
Note: You can also implement a function to find the square root of a number on your own, but here will use the in-built STL methods provided by each language.
Algorithm
- Return the square root of
n.