Rotting oranges
class Solution:
def __init__(self):
self.visited = set()
self.directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]
self.start = []
self.totalCount = 0
self.time = 0
def bfs(self, grid):
q = collections.deque(self.start)
while q:
size = len(q)
for i in range(size):
x, y, self.time = q.popleft()
for dx, dy in self.directions:
newx = x + dx
newy = y + dy
if 0 <= newx < len(grid) and 0 <= newy < len(grid[0]):
if (newx, newy) not in self.visited and grid[newx][newy] == 1:
q.append((newx, newy, self.time + 1))
self.visited.add((newx, newy))
grid[newx][newy] = 2
def orangesRotting(self, grid: List[List[int]]) -> int:
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j] == 2:
self.start.append((i, j, 0))
self.visited.add((i, j))
if grid[i][j] == 1:
self.totalCount += 1
self.bfs(grid)
for row in grid:
if 1 in row:
return -1
return self.time
Rotting Oranges
You are given an m x n grid where each cell can have one of three values:
0representing an empty cell,1representing a fresh orange, or2representing a rotten orange.
Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.
Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.
Example 1:
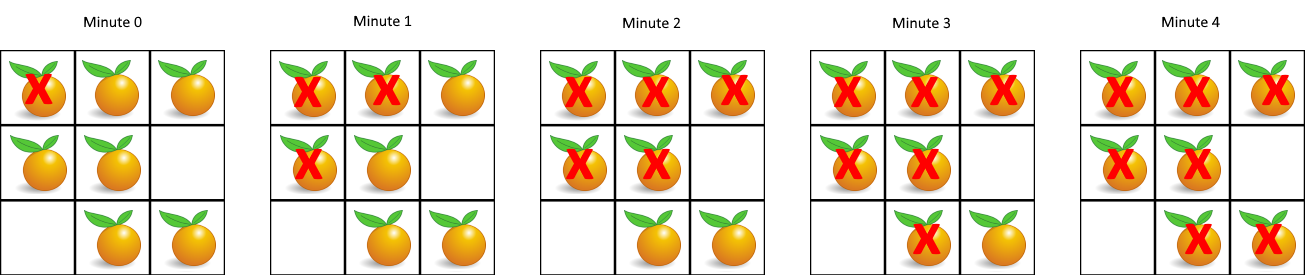
Input: grid = [[2,1,1],[1,1,0],[0,1,1]] Output: 4
Example 2:
Input: grid = [[2,1,1],[0,1,1],[1,0,1]] Output: -1 Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.
Example 3:
Input: grid = [[0,2]] Output: 0 Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0.
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 10grid[i][j]is0,1, or2.
