Number of enclaves

class Solution:
    def __init__(self):
        self.res = 0
        self.curr = 0
        self.visited = set()
        self.directions = [(0, 1), (0, -1), (-1, 0), (1, 0)]
        self.isValid = True

    def dfs(self, grid, i, j):
        for dx, dy in self.directions:
            x, y = i + dx, j + dy
            if 0 <= x < len(grid) and 0 <= y < len(grid[0]):
                if (x, y) not in self.visited and grid[x][y] == 1:
                    if x == 0 or x == len(grid) - 1 or y == 0 or y == len(grid[0]) - 1:
                        self.isValid = False
                    self.visited.add((x, y))
                    self.curr += 1
                    self.dfs(grid, x, y)

    def numEnclaves(self, grid: List[List[int]]) -> int:
        for i in range(1, len(grid) - 1):
            for j in range(1, len(grid[0]) - 1):
                if (i, j) not in self.visited and grid[i][j] == 1:
                    self.visited.add((i, j))
                    self.curr = 1
                    self.isValid = True
                    self.dfs(grid, i, j)
                    if self.isValid:
                        self.res += self.curr

        return self.res

Number of Enclaves

---

You are given an m x n binary matrix grid, where 0 represents a sea cell and 1 represents a land cell.

A move consists of walking from one land cell to another adjacent (4-directionally) land cell or walking off the boundary of the grid.

Return the number of land cells in grid for which we cannot walk off the boundary of the grid in any number of moves.

 

Example 1:

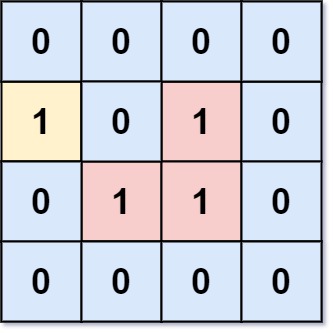
Input: grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
Output: 3
Explanation: There are three 1s that are enclosed by 0s, and one 1 that is not enclosed because its on the boundary.

Example 2:

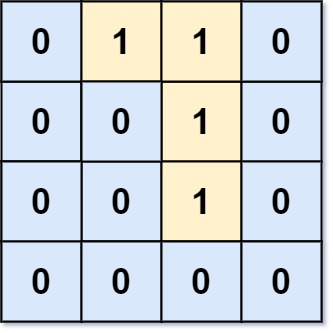
Input: grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
Output: 0
Explanation: All 1s are either on the boundary or can reach the boundary.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 500
• grid[i][j] is either 0 or 1.