Binary tree maximum path sum

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxPathSum(self, root: Optional[TreeNode]) -> int:
        res = [-math.inf]
        def helper(node):
            if not node:
                return 0
            left = max(helper(node.left), 0)
            right = max(helper(node.right), 0)
            res[0] = max(
                res[0],
                left + right + node.val
            )
            return max(
                node.val + right,
                node.val + left
            )
        helper(root)
        return res[0]








# class Solution:
#     def max_path_sum(self, root: Optional[TreeNode]) -> int:
#         max_path = -float('inf')

#         # post order traversal of subtree rooted at `node`
#         def gain_from_subtree(node: Optional[TreeNode]) -> int:
#             nonlocal max_path

#             if not node:
#                 return 0

#             # add the gain from the left subtree. Note that if the
#             # gain is negative, we can ignore it, or count it as 0.
#             # This is the reason we use `max` here.
#             gain_from_left = max(gain_from_subtree(node.left), 0)

#             # add the gain / path sum from right subtree. 0 if negative
#             gain_from_right = max(gain_from_subtree(node.right), 0)

#             # if left or right gain are negative, they are counted
#             # as 0, so this statement takes care of all four scenarios
#             max_path = max(max_path, gain_from_left + gain_from_right + node.val)

#             # return the max sum for a path starting at the root of subtree
#             return max(
#                 gain_from_left + node.val,
#                 gain_from_right + node.val
#             )

#         gain_from_subtree(root)
#         return max_path

Binary Tree Maximum Path Sum

A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.

The path sum of a path is the sum of the node's values in the path.

Given the root of a binary tree, return the maximum path sum of any non-empty path.

Example 1:

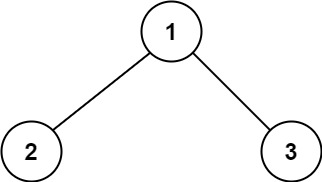
Input: root = [1,2,3]
Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.

Example 2:

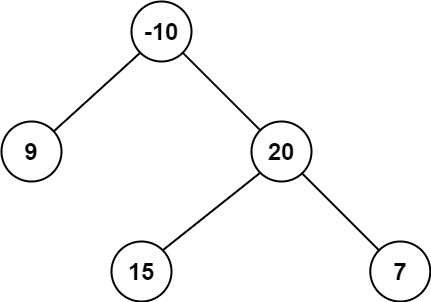
Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

Constraints:

The number of nodes in the tree is in the range [1, 3 * 10⁴].
-1000 <= Node.val <= 1000