Graph valid tree

class Solution:
    def validTree(self, n: int, edges: List[List[int]]) -> bool:
        if not n:
            return False

        # graph construction
        graph = [[] for _ in range(n)]
        for u, v in edges:
            graph[u].append(v)
            graph[v].append(u)

        visited = [False] * n
        queue = deque([(0, -1)])  # Queue of tuples (node, parent)
        visited[0] = True

        # BFS
        while queue:
            node, parent = queue.popleft()
            for neighbor in graph[node]:
                if visited[neighbor]:
                    if neighbor != parent:  # Detect cycle
                        return False
                    continue
                visited[neighbor] = True
                queue.append((neighbor, node))


        # Check if the graph is connected
        return all(visited)

Graph Valid Tree

You have a graph of n nodes labeled from 0 to n - 1. You are given an integer n and a list of edges where edges[i] = [a_i, b_i] indicates that there is an undirected edge between nodes a_i and b_i in the graph.

Return true if the edges of the given graph make up a valid tree, and false otherwise.

Example 1:

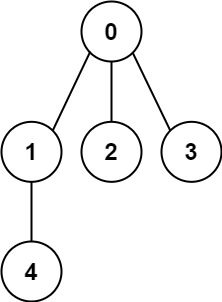
Input: n = 5, edges = [[0,1],[0,2],[0,3],[1,4]]
Output: true

Example 2:

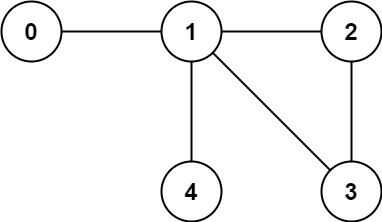
Input: n = 5, edges = [[0,1],[1,2],[2,3],[1,3],[1,4]]
Output: false

Constraints:

1 <= n <= 2000
0 <= edges.length <= 5000
edges[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
There are no self-loops or repeated edges.