Number of connected components in an undirected graph

class UF():
    def __init__(self, n) -> None:
        self.parents = [i for i in range(n)]
        self.count = n

    def find(self, x):
        if x != self.parents[x]:
            self.parents[x] = self.find(self.parents[x])
        return self.parents[x]

    def union(self, a, b):
        roota = self.find(a)
        rootb = self.find(b)

        if roota == rootb:
            self.count -= 0
            return

        self.parents[rootb] = roota
        self.count -= 1

class Solution:
    def countComponents(self, n: int, edges: List[List[int]]) -> int:
        uf = UF(n)
        for v, u in edges:
            uf.union(v, u)
        return uf.count

Number of Connected Components in an Undirected Graph

---

You have a graph of n nodes. You are given an integer n and an array edges where edges[i] = [ai, bi] indicates that there is an edge between ai and bi in the graph.

Return the number of connected components in the graph.

 

Example 1:

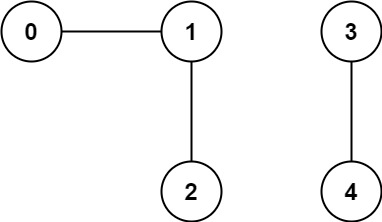
Input: n = 5, edges = [[0,1],[1,2],[3,4]]
Output: 2

Example 2:

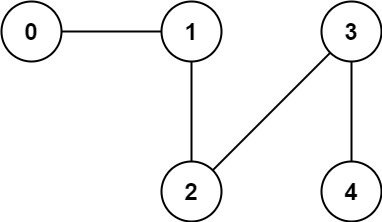
Input: n = 5, edges = [[0,1],[1,2],[2,3],[3,4]]
Output: 1

 

Constraints:

• 1 <= n <= 2000
• 1 <= edges.length <= 5000
• edges[i].length == 2
• 0 <= ai <= bi < n
• ai != bi
• There are no repeated edges.