Pacific atlantic water flow

class Solution:
    def pacificAtlantic(self, heights: List[List[int]]) -> List[List[int]]:
        pacific = set()
        atlantic = set()
        rows = len(heights)
        cols = len(heights[0])

        def dfs(i, j, reachable):
            reachable.add((i, j))
            for (x, y) in [(1, 0), (0, 1), (-1, 0), (0, -1)]:
                newx, newy = i + x, j + y
                if 0 <= newx < rows and 0 <= newy < cols:
                    if (newx, newy) not in reachable:
                        if heights[newx][newy] >= heights[i][j]:
                            dfs(newx, newy, reachable)
        for i in range(rows):
            dfs(i, 0, pacific)
            dfs(i, cols - 1, atlantic)
        for i in range(cols):
            dfs(0, i, pacific)
            dfs(rows - 1, i, atlantic)
        return list(pacific.intersection(atlantic))


# class Solution:
#     def pacificAtlantic(self, matrix: List[List[int]]) -> List[List[int]]:
#         # Check if input is empty
#         if not matrix or not matrix[0]: 
#             return []

#         # Initialize variables, including sets used to keep track of visited cells
#         num_rows, num_cols = len(matrix), len(matrix[0])
#         pacific_reachable = set()
#         atlantic_reachable = set()

#         def dfs(row, col, reachable):
#             # This cell is reachable, so mark it
#             reachable.add((row, col))
#             for (x, y) in [(1, 0), (0, 1), (-1, 0), (0, -1)]: # Check all 4 directions
#                 new_row, new_col = row + x, col + y
#                 # Check if the new cell is within bounds
#                 if new_row < 0 or new_row >= num_rows or new_col < 0 or new_col >= num_cols:
#                     continue
#                 # Check that the new cell hasn't already been visited
#                 if (new_row, new_col) in reachable:
#                     continue
#                 # Check that the new cell has a higher or equal height,
#                 # So that water can flow from the new cell to the old cell
#                 if matrix[new_row][new_col] < matrix[row][col]:
#                     continue
#                 # If we've gotten this far, that means the new cell is reachable
#                 dfs(new_row, new_col, reachable)

#         # Loop through each cell adjacent to the oceans and start a DFS
#         for i in range(num_rows):
#             dfs(i, 0, pacific_reachable)
#             dfs(i, num_cols - 1, atlantic_reachable)
#         for i in range(num_cols):
#             dfs(0, i, pacific_reachable)
#             dfs(num_rows - 1, i, atlantic_reachable)

#         # Find all cells that can reach both oceans, and convert to list
#         return list(pacific_reachable.intersection(atlantic_reachable))

Pacific Atlantic Water Flow

There is an m x n rectangular island that borders both the Pacific Ocean and Atlantic Ocean. The Pacific Ocean touches the island's left and top edges, and the Atlantic Ocean touches the island's right and bottom edges.

The island is partitioned into a grid of square cells. You are given an m x n integer matrix heights where heights[r][c] represents the height above sea level of the cell at coordinate (r, c).

The island receives a lot of rain, and the rain water can flow to neighboring cells directly north, south, east, and west if the neighboring cell's height is less than or equal to the current cell's height. Water can flow from any cell adjacent to an ocean into the ocean.

Return a 2D list of grid coordinates result where result[i] = [r_i, c_i] denotes that rain water can flow from cell (r_i, c_i) to both the Pacific and Atlantic oceans.

Example 1:

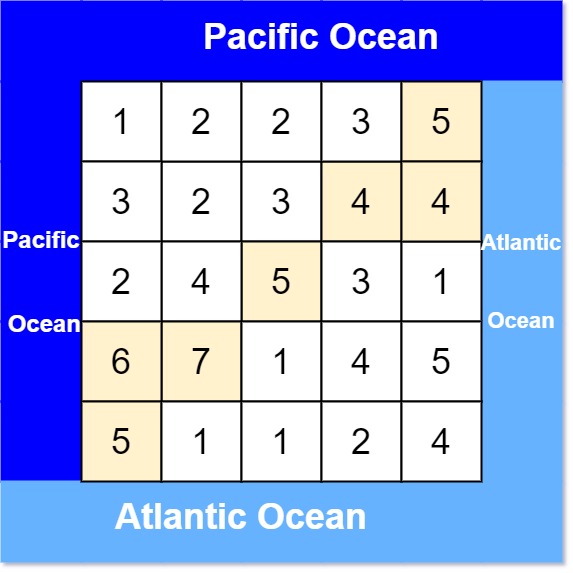
Input: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]]
Output: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]
Explanation: The following cells can flow to the Pacific and Atlantic oceans, as shown below:
[0,4]: [0,4] -> Pacific Ocean 
       [0,4] -> Atlantic Ocean
[1,3]: [1,3] -> [0,3] -> Pacific Ocean 
       [1,3] -> [1,4] -> Atlantic Ocean
[1,4]: [1,4] -> [1,3] -> [0,3] -> Pacific Ocean 
       [1,4] -> Atlantic Ocean
[2,2]: [2,2] -> [1,2] -> [0,2] -> Pacific Ocean 
       [2,2] -> [2,3] -> [2,4] -> Atlantic Ocean
[3,0]: [3,0] -> Pacific Ocean 
       [3,0] -> [4,0] -> Atlantic Ocean
[3,1]: [3,1] -> [3,0] -> Pacific Ocean 
       [3,1] -> [4,1] -> Atlantic Ocean
[4,0]: [4,0] -> Pacific Ocean 
       [4,0] -> Atlantic Ocean
Note that there are other possible paths for these cells to flow to the Pacific and Atlantic oceans.

Example 2:

Input: heights = [[1]]
Output: [[0,0]]
Explanation: The water can flow from the only cell to the Pacific and Atlantic oceans.

Constraints:

m == heights.length
n == heights[r].length
1 <= m, n <= 200
0 <= heights[r][c] <= 10⁵