Trim a binary search tree

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def trimBST(self, root: Optional[TreeNode], low: int, high: int) -> Optional[TreeNode]:
        if not root:
            return None
        if root.val < low:
            right = self.trimBST(root.right, low, high)
            return right
        if root.val > high:
            left = self.trimBST(root.left, low, high)
            return left

        root.left = self.trimBST(root.left, low, high)
        root.right = self.trimBST(root.right, low, high)

        return root

Trim a Binary Search Tree

Given the root of a binary search tree and the lowest and highest boundaries as low and high, trim the tree so that all its elements lies in [low, high]. Trimming the tree should not change the relative structure of the elements that will remain in the tree (i.e., any node's descendant should remain a descendant). It can be proven that there is a unique answer.

Return the root of the trimmed binary search tree. Note that the root may change depending on the given bounds.

Example 1:

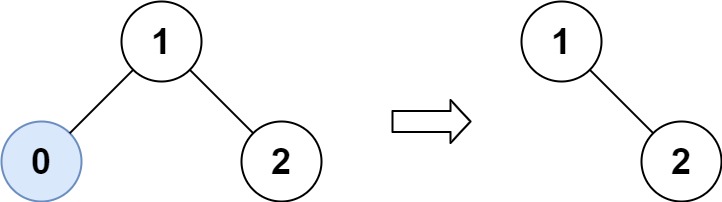
Input: root = [1,0,2], low = 1, high = 2
Output: [1,null,2]

Example 2:

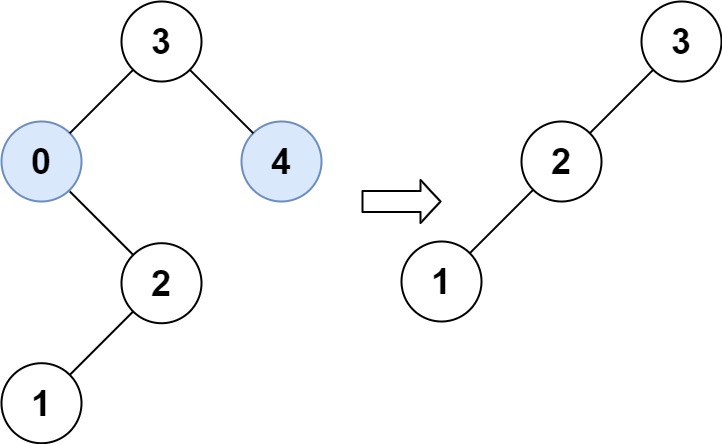
Input: root = [3,0,4,null,2,null,null,1], low = 1, high = 3
Output: [3,2,null,1]

Constraints:

The number of nodes in the tree is in the range [1, 10⁴].
0 <= Node.val <= 10⁴
The value of each node in the tree is unique.
root is guaranteed to be a valid binary search tree.
0 <= low <= high <= 10⁴