图论深搜理论基础

参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！

# 深度优先搜索理论基础 录友们期待图论内容已久了，为什么鸽了这么久，主要是最近半年开始更新[代码随想录算法公开课](https://www.bilibili.com/video/BV1fA4y1o715/)，是开源在B站的算法视频，已经帮助非常多基础不好的录友学习算法。 录视频其实是非常累的，也要花很多时间，所以图论这边就没抽出时间来。 后面计划先给大家讲图论里大家特别需要的深搜和广搜。 以下，开始讲解深度优先搜索理论基础： ## dfs 与 bfs 区别 提到深度优先搜索（dfs），就不得不说和广度优先搜索（bfs）有什么区别 先来了解dfs的过程，很多录友可能对dfs（深度优先搜索），bfs（广度优先搜索）分不清。 先给大家说一下两者大概的区别： * dfs是可一个方向去搜，不到黄河不回头，直到遇到绝境了，搜不下去了，再换方向（换方向的过程就涉及到了回溯）。 * bfs是先把本节点所连接的所有节点遍历一遍，走到下一个节点的时候，再把连接节点的所有节点遍历一遍，搜索方向更像是广度，四面八方的搜索过程。 当然以上讲的是，大体可以这么理解，接下来 我们详细讲解dfs，（bfs在用单独一篇文章详细讲解） ## dfs 搜索过程 上面说道dfs是可一个方向搜，不到黄河不回头。 那么我们来举一个例子。 如图一，是一个无向图，我们要搜索从节点1到节点6的所有路径。 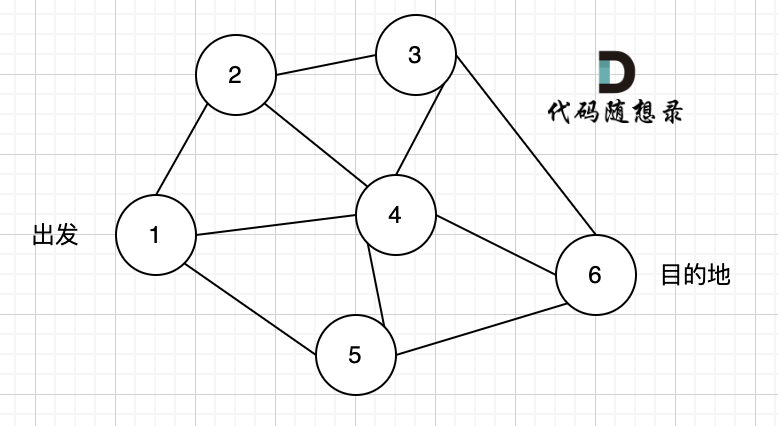 那么dfs搜索的第一条路径是这样的： （假设第一次延默认方向，就找到了节点6），图二 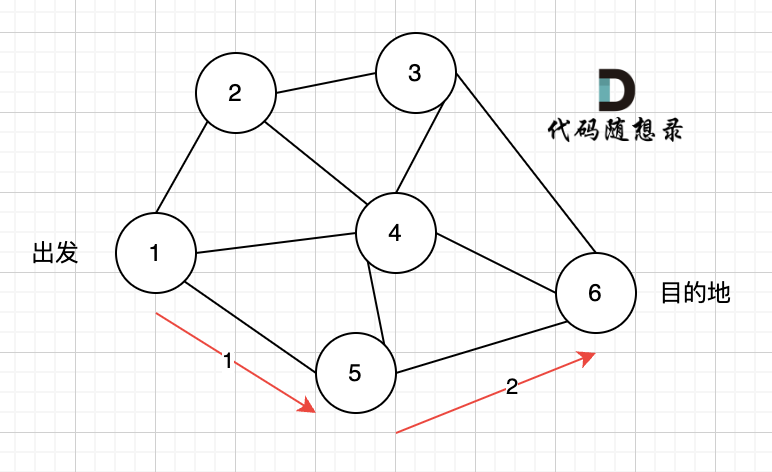 此时我们找到了节点6，（遇到黄河了，是不是应该回头了），那么应该再去搜索其他方向了。 如图三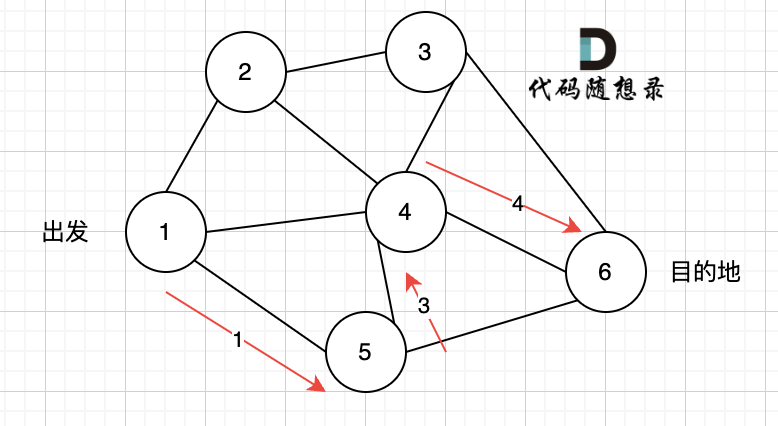：  路径2撤销了，改变了方向，走路径3（红色线）， 接着也找到终点6。 那么撤销路径2，改为路径3，在dfs中其实就是回溯的过程（这一点很重要，很多录友不理解dfs代码中回溯是用来干什么的） 又找到了一条从节点1到节点6的路径，又到黄河了，此时再回头，下图图四中，路径4撤销（回溯的过程），改为路径5。 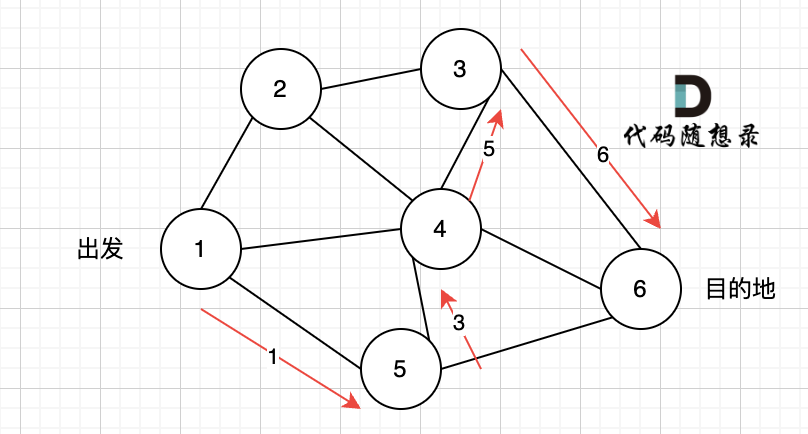 又找到了一条从节点1到节点6的路径，又到黄河了，此时再回头，下图图五，路径6撤销（回溯的过程），改为路径7，路径8 和 路径7，路径9， 结果发现死路一条，都走到了自己走过的节点。 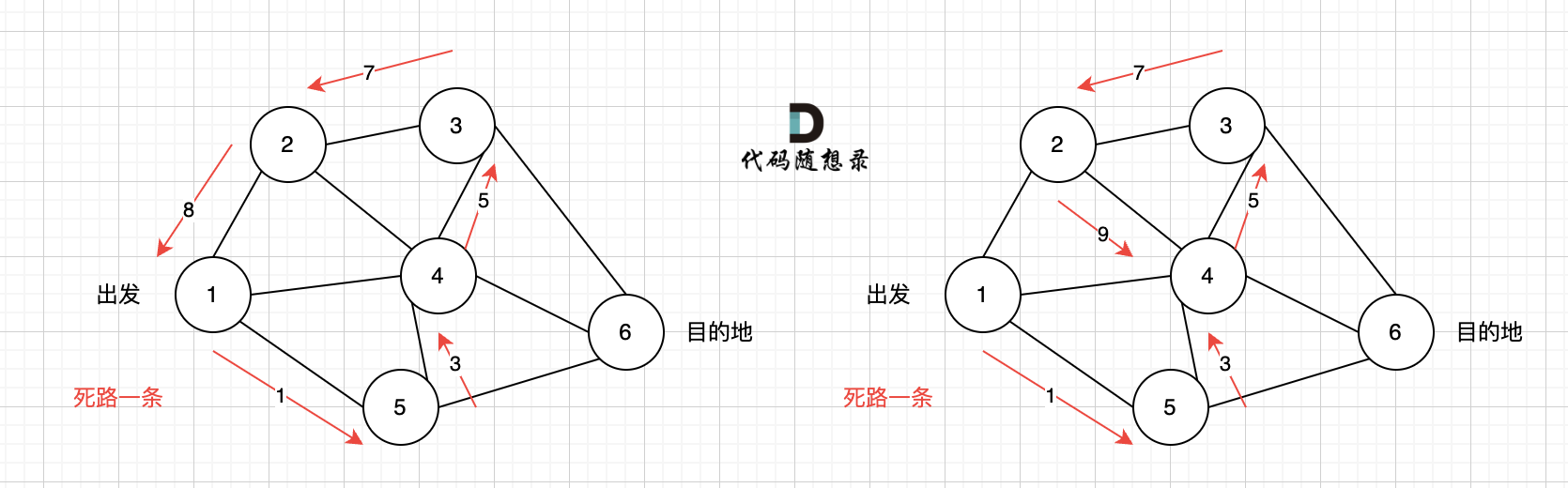 那么节点2所连接路径和节点3所链接的路径 都走过了，撤销路径只能向上回退，去选择撤销当初节点4的选择，也就是撤销路径5，改为路径10 。 如图图六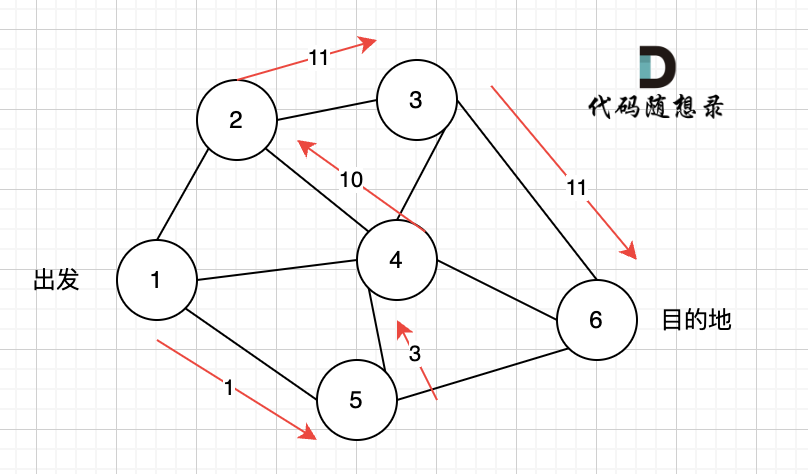：  上图演示中，其实我并没有把 所有的 从节点1 到节点6的dfs（深度优先搜索）的过程都画出来，那样太冗余了，但 已经把dfs 关键的地方都涉及到了，关键就两点： * 搜索方向，是认准一个方向搜，直到碰壁之后再换方向 * 换方向是撤销原路径，改为节点链接的下一个路径，回溯的过程。 ## 代码框架 正是因为dfs搜索可一个方向，并需要回溯，所以用递归的方式来实现是最方便的。 很多录友对回溯很陌生，建议先看看代码随想录，[回溯算法章节](https://programmercarl.com/回溯算法理论基础.html)。 有递归的地方就有回溯，那么回溯在哪里呢？ 就地递归函数的下面，例如如下代码：

void dfs(参数) {
    处理节点
    dfs(图，选择的节点); // 递归
    回溯，撤销处理结果
}

可以看到回溯操作就在递归函数的下面，递归和回溯是相辅相成的。 在讲解[二叉树章节](https://programmercarl.com/二叉树理论基础.html)的时候，二叉树的递归法其实就是dfs，而二叉树的迭代法，就是bfs（广度优先搜索） 所以**dfs，bfs其实是基础搜索算法，也广泛应用与其他数据结构与算法中**。 我们在回顾一下[回溯法](https://programmercarl.com/回溯算法理论基础.html)的代码框架：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }
    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

回溯算法，其实就是dfs的过程，这里给出dfs的代码框架：

void dfs(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本节点所连接的其他节点) {
        处理节点;
        dfs(图，选择的节点); // 递归
        回溯，撤销处理结果
    }
}

可以发现dfs的代码框架和回溯算法的代码框架是差不多的。 下面我在用 深搜三部曲，来解读 dfs的代码框架。 ## 深搜三部曲 在 [二叉树递归讲解](https://programmercarl.com/%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E9%80%92%E5%BD%92%E9%81%8D%E5%8E%86.html)中，给出了递归三部曲。 [回溯算法](https://programmercarl.com/回溯算法理论基础.html)讲解中，给出了 回溯三部曲。 其实深搜也是一样的，深搜三部曲如下： 1. 确认递归函数，参数

void dfs(参数)

通常我们递归的时候，我们递归搜索需要了解哪些参数，其实也可以在写递归函数的时候，发现需要什么参数，再去补充就可以。 一般情况，深搜需要 二维数组数组结构保存所有路径，需要一维数组保存单一路径，这种保存结果的数组，我们可以定义一个全局变量，避免让我们的函数参数过多。 例如这样：

vector<vector<int>> result; // 保存符合条件的所有路径
vector<int> path; // 起点到终点的路径
void dfs (图，目前搜索的节点)  

但这种写法看个人习惯，不强求。 2. 确认终止条件 终止条件很重要，很多同学写dfs的时候，之所以容易死循环，栈溢出等等这些问题，都是因为终止条件没有想清楚。

if (终止条件) {
    存放结果;
    return;
}

终止添加不仅是结束本层递归，同时也是我们收获结果的时候。 另外，其实很多dfs写法，没有写终止条件，其实终止条件写在了， 下面dfs递归的逻辑里了，也就是不符合条件，直接不会向下递归。这里如果大家不理解的话，没关系，后面会有具体题目来讲解。 3. 处理目前搜索节点出发的路径 一般这里就是一个for循环的操作，去遍历 目前搜索节点 所能到的所有节点。

for (选择：本节点所连接的其他节点) {
    处理节点;
    dfs(图，选择的节点); // 递归
    回溯，撤销处理结果
}

不少录友疑惑的地方，都是 dfs代码框架中for循环里分明已经处理节点了，那么 dfs函数下面 为什么还要撤销的呢。 如图七所示， 路径2 已经走到了 目的地节点6，那么 路径2 是如何撤销，然后改为 路径3呢？ 其实这就是 回溯的过程，撤销路径2，走换下一个方向。  ## 总结 我们讲解了，dfs 和 bfs的大体区别（bfs详细过程下篇来讲），dfs的搜索过程以及代码框架。 最后还有 深搜三部曲来解读这份代码框架。 以上如果大家都能理解了，其实搜索的代码就很好写，具体题目套用具体场景就可以了。 后面我也会给大家安排具体练习的题目，依旧是代码随想录的风格，循序渐进由浅入深！