0070.爬楼梯
参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
# 70. 爬楼梯 [力扣题目链接](https://leetcode.cn/problems/climbing-stairs/) 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？ 注意：给定 n 是一个正整数。 示例 1： * 输入： 2 * 输出： 2 * 解释： 有两种方法可以爬到楼顶。 * 1 阶 + 1 阶 * 2 阶 示例 2： * 输入： 3 * 输出： 3 * 解释： 有三种方法可以爬到楼顶。 * 1 阶 + 1 阶 + 1 阶 * 1 阶 + 2 阶 * 2 阶 + 1 阶 ## 算法公开课 **[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html)：[带你学透动态规划-爬楼梯|LeetCode:70.爬楼梯）](https://www.bilibili.com/video/BV17h411h7UH)，相信结合视频在看本篇题解，更有助于大家对本题的理解**。 ## 思路 本题大家如果没有接触过的话，会感觉比较难，多举几个例子，就可以发现其规律。 爬到第一层楼梯有一种方法，爬到二层楼梯有两种方法。 那么第一层楼梯再跨两步就到第三层 ，第二层楼梯再跨一步就到第三层。 所以到第三层楼梯的状态可以由第二层楼梯 和 到第一层楼梯状态推导出来，那么就可以想到动态规划了。 我们来分析一下，动规五部曲： 定义一个一维数组来记录不同楼层的状态 1. 确定dp数组以及下标的含义 dp[i]： 爬到第i层楼梯，有dp[i]种方法 2. 确定递推公式 如何可以推出dp[i]呢？ 从dp[i]的定义可以看出，dp[i] 可以有两个方向推出来。 首先是dp[i - 1]，上i-1层楼梯，有dp[i - 1]种方法，那么再一步跳一个台阶不就是dp[i]了么。 还有就是dp[i - 2]，上i-2层楼梯，有dp[i - 2]种方法，那么再一步跳两个台阶不就是dp[i]了么。 那么dp[i]就是 dp[i - 1]与dp[i - 2]之和！ 所以dp[i] = dp[i - 1] + dp[i - 2] 。 在推导dp[i]的时候，一定要时刻想着dp[i]的定义，否则容易跑偏。 这体现出确定dp数组以及下标的含义的重要性！ 3. dp数组如何初始化 再回顾一下dp[i]的定义：爬到第i层楼梯，有dp[i]种方法。 那么i为0，dp[i]应该是多少呢，这个可以有很多解释，但基本都是直接奔着答案去解释的。 例如强行安慰自己爬到第0层，也有一种方法，什么都不做也就是一种方法即：dp[0] = 1，相当于直接站在楼顶。 但总有点牵强的成分。 那还这么理解呢：我就认为跑到第0层，方法就是0啊，一步只能走一个台阶或者两个台阶，然而楼层是0，直接站楼顶上了，就是不用方法，dp[0]就应该是0. **其实这么争论下去没有意义，大部分解释说dp[0]应该为1的理由其实是因为dp[0]=1的话在递推的过程中i从2开始遍历本题就能过，然后就往结果上靠去解释dp[0] = 1**。 从dp数组定义的角度上来说，dp[0] = 0 也能说得通。 需要注意的是：题目中说了n是一个正整数，题目根本就没说n有为0的情况。 所以本题其实就不应该讨论dp[0]的初始化！ 我相信dp[1] = 1，dp[2] = 2，这个初始化大家应该都没有争议的。 所以我的原则是：不考虑dp[0]如何初始化，只初始化dp[1] = 1，dp[2] = 2，然后从i = 3开始递推，这样才符合dp[i]的定义。 4. 确定遍历顺序 从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出，遍历顺序一定是从前向后遍历的 5. 举例推导dp数组 举例当n为5的时候，dp table（dp数组）应该是这样的 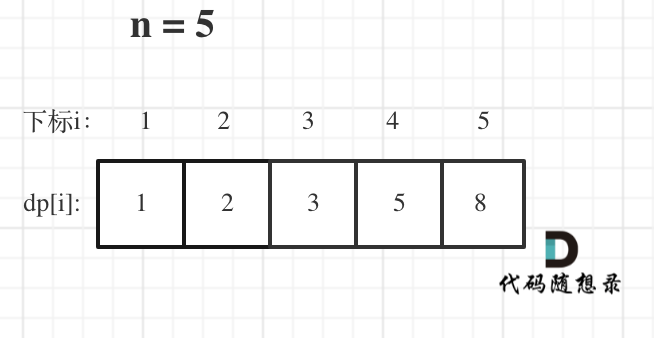 如果代码出问题了，就把dp table 打印出来，看看究竟是不是和自己推导的一样。 **此时大家应该发现了，这不就是斐波那契数列么！** 唯一的区别是，没有讨论dp[0]应该是什么，因为dp[0]在本题没有意义！ 以上五部分析完之后，C++代码如下：// 版本一
class Solution {
public:
int climbStairs(int n) {
if (n <= 1) return n; // 因为下面直接对dp[2]操作了，防止空指针
vector<int> dp(n + 1);
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) { // 注意i是从3开始的
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
};
// 版本二
class Solution {
public:
int climbStairs(int n) {
if (n <= 1) return n;
int dp[3];
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) {
int sum = dp[1] + dp[2];
dp[1] = dp[2];
dp[2] = sum;
}
return dp[2];
}
};
class Solution {
public:
int climbStairs(int n) {
vector<int> dp(n + 1, 0);
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) { // 把m换成2，就可以AC爬楼梯这道题
if (i - j >= 0) dp[i] += dp[i - j];
}
}
return dp[n];
}
};
// 常规方式
public int climbStairs(int n) {
int[] dp = new int[n + 1];
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
// 用变量记录代替数组
class Solution {
public int climbStairs(int n) {
if(n <= 2) return n;
int a = 1, b = 2, sum = 0;
for(int i = 3; i <= n; i++){
sum = a + b; // f(i - 1) + f(i - 2)
a = b; // 记录f(i - 1)，即下一轮的f(i - 2)
b = sum; // 记录f(i)，即下一轮的f(i - 1)
}
return b;
}
}
# 空间复杂度为O(n)版本
class Solution:
def climbStairs(self, n: int) -> int:
if n <= 1:
return n
dp = [0] * (n + 1)
dp[1] = 1
dp[2] = 2
for i in range(3, n + 1):
dp[i] = dp[i - 1] + dp[i - 2]
return dp[n]
# 空间复杂度为O(3)版本
class Solution:
def climbStairs(self, n: int) -> int:
if n <= 1:
return n
dp = [0] * 3
dp[1] = 1
dp[2] = 2
for i in range(3, n + 1):
total = dp[1] + dp[2]
dp[1] = dp[2]
dp[2] = total
return dp[2]
# 空间复杂度为O(1)版本
class Solution:
def climbStairs(self, n: int) -> int:
if n <= 1:
return n
prev1 = 1
prev2 = 2
for i in range(3, n + 1):
total = prev1 + prev2
prev1 = prev2
prev2 = total
return prev2
func climbStairs(n int) int {
if n == 1 {
return 1
}
dp := make([]int, n+1)
dp[1] = 1
dp[2] = 2
for i := 3; i <= n; i++ {
dp[i] = dp[i-1] + dp[i-2]
}
return dp[n]
}
var climbStairs = function(n) {
// dp[i] 为第 i 阶楼梯有多少种方法爬到楼顶
// dp[i] = dp[i - 1] + dp[i - 2]
let dp = [1 , 2]
for(let i = 2; i < n; i++) {
dp[i] = dp[i - 1] + dp[i - 2]
}
return dp[n - 1]
};
function climbStairs(n: number): number {
/**
dp[i]: i阶楼梯的方法种数
dp[1]: 1;
dp[2]: 2;
...
dp[i]: dp[i - 1] + dp[i - 2];
*/
const dp: number[] = [];
dp[1] = 1;
dp[2] = 2;
for (let i = 3; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
};
function climbStairs(n: number): number {
/**
一次可以爬m阶
dp[i]: i阶楼梯的方法种数
dp[1]: 1;
dp[2]: 2;
dp[3]: dp[2] + dp[1];
...
dp[i]: dp[i - 1] + dp[i - 2] + ... + dp[max(i - m, 1)]; 从i-1加到max(i-m, 1)
*/
const m: number = 2; // 本题m为2
const dp: number[] = new Array(n + 1).fill(0);
dp[1] = 1;
dp[2] = 2;
for (let i = 3; i <= n; i++) {
const end: number = Math.max(i - m, 1);
for (let j = i - 1; j >= end; j--) {
dp[i] += dp[j];
}
}
return dp[n];
};
int climbStairs(int n){
//若n<=2，返回n
if(n <= 2)
return n;
//初始化dp数组，数组大小为n+1
int *dp = (int *)malloc(sizeof(int) * (n + 1));
dp[0] = 0, dp[1] = 1, dp[2] = 2;
//从前向后遍历数组，dp[i] = dp[i-1] + dp[i-2]
int i;
for(i = 3; i <= n; ++i) {
dp[i] = dp[i - 1] + dp[i - 2];
}
//返回dp[n]
return dp[n];
}
int climbStairs(int n){
//若n<=2，返回n
if(n <= 2)
return n;
//初始化dp数组，数组大小为3
int *dp = (int *)malloc(sizeof(int) * 3);
dp[1] = 1, dp[2] = 2;
//只记录前面两个台阶的状态
int i;
for(i = 3; i <= n; ++i) {
int sum = dp[1] + dp[2];
dp[1] = dp[2];
dp[2] = sum;
}
//返回dp[2]
return dp[2];
}
object Solution {
def climbStairs(n: Int): Int = {
if (n <= 2) return n
var dp = new Array[Int](n + 1)
dp(1) = 1
dp(2) = 2
for (i <- 3 to n) {
dp(i) = dp(i - 1) + dp(i - 2)
}
dp(n)
}
}
object Solution {
def climbStairs(n: Int): Int = {
if (n <= 2) return n
var (a, b) = (1, 2)
for (i <- 3 to n) {
var tmp = a + b
a = b
b = tmp
}
b // 最终返回b
}
}
public class Solution {
public int ClimbStairs(int n) {
if(n<=2) return n;
int[] dp = new int[2] { 1, 2 };
for (int i = 3; i <= n; i++)
{
int temp = dp[0] + dp[1];
dp[0] = dp[1];
dp[1] = temp;
}
return dp[1];
}
}
impl Solution {
pub fn climb_stairs(n: i32) -> i32 {
if n <= 1 {
return n;
}
let (mut a, mut b, mut f) = (1, 1, 0);
for _ in 2..=n {
f = a + b;
a = b;
b = f;
}
f
}
impl Solution {
pub fn climb_stairs(n: i32) -> i32 {
let n = n as usize;
let mut dp = vec![0; n + 1];
dp[0] = 1;
dp[1] = 1;
for i in 2..=n {
dp[i] = dp[i - 1] + dp[i - 2];
}
dp[n]
}
}
