0841.钥匙和房间
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
# 841.钥匙和房间 [力扣题目链接](https://leetcode.cn/problems/keys-and-rooms/) 有 N 个房间,开始时你位于 0 号房间。每个房间有不同的号码:0,1,2,...,N-1,并且房间里可能有一些钥匙能使你进入下一个房间。 在形式上,对于每个房间 i 都有一个钥匙列表 rooms[i],每个钥匙 rooms[i][j] 由 [0,1,...,N-1] 中的一个整数表示,其中 N = rooms.length。 钥匙 rooms[i][j] = v 可以打开编号为 v 的房间。 最初,除 0 号房间外的其余所有房间都被锁住。 你可以自由地在房间之间来回走动。 如果能进入每个房间返回 true,否则返回 false。 示例 1: * 输入: [[1],[2],[3],[]] * 输出: true * 解释: 我们从 0 号房间开始,拿到钥匙 1。 之后我们去 1 号房间,拿到钥匙 2。 然后我们去 2 号房间,拿到钥匙 3。 最后我们去了 3 号房间。 由于我们能够进入每个房间,我们返回 true。 示例 2: * 输入:[[1,3],[3,0,1],[2],[0]] * 输出:false * 解释:我们不能进入 2 号房间。 ## 思路 本题其实给我们是一个有向图, 意识到这是有向图很重要! 图中给我的两个示例: `[[1],[2],[3],[]]` `[[1,3],[3,0,1],[2],[0]]`,画成对应的图如下: 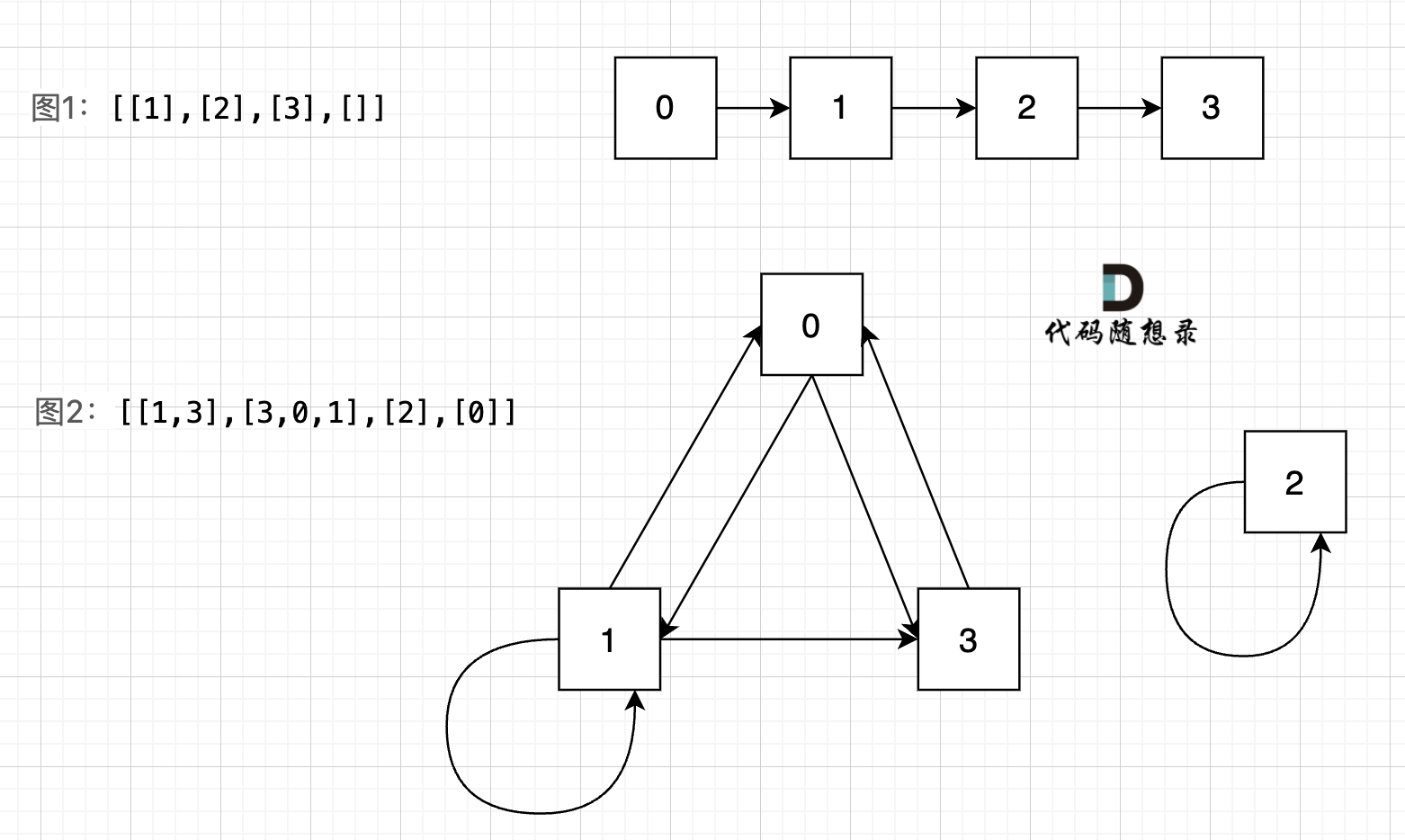 我们可以看出图1的所有节点都是链接的,而图二中,节点2 是孤立的。 这就很容易让我们想起岛屿问题,只要发现独立的岛,就是不能进入所有房间。 此时也容易想到用并查集的方式去解决。 **但本题是有向图**,在有向图中,即使所有节点都是链接的,但依然不可能从0出发遍历所有边。 给大家举一个例子: 图3:[[5], [], [1, 3], [5]] ,如图: 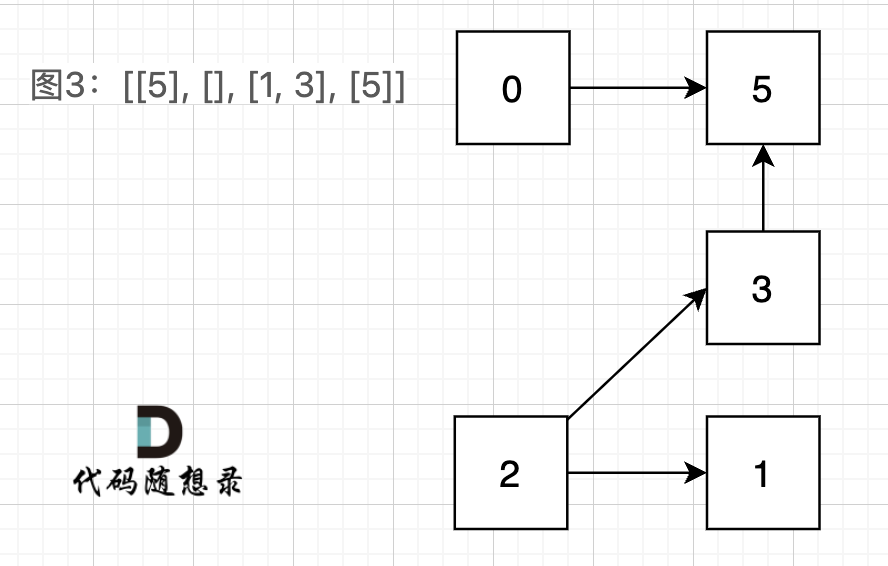 在图3中,大家可以发现,节点0只能到节点5,然后就哪也去不了了。 所以本题是一个有向图搜索全路径的问题。 只能用深搜(DFS)或者广搜(BFS)来搜。 关于DFS的理论,如果大家有困惑,可以先看我这篇题解: [DFS理论基础](https://programmercarl.com/图论深搜理论基础.html) **以下dfs分析 大家一定要仔细看,本题有两种dfs的解法,很多题解没有讲清楚**。 看完之后 相信你对dfs会有更深的理解。 深搜三部曲: 1. 确认递归函数,参数 需要传入二维数组rooms来遍历地图,需要知道当前我们拿到的key,以至于去下一个房间。 同时还需要一个数组,用来记录我们都走过了哪些房间,这样好知道最后有没有把所有房间都遍历的,可以定义一个一维数组。 所以 递归函数参数如下:// key 当前得到的可以
// visited 记录访问过的房间
void dfs(const vector<vector<int>>& rooms, int key, vector<bool>& visited) {
// 写法一:处理当前访问的节点
void dfs(const vector<vector<int>>& rooms, int key, vector<bool>& visited) {
if (visited[key]) { // 本层递归是true,说明访问过,立刻返回
return;
}
visited[key] = true; // 给当前遍历的节点赋值true
vector<int> keys = rooms[key];
for (int key : keys) {
// 深度优先搜索遍历
dfs(rooms, key, visited);
}
}
// 写法二:处理下一个要访问的节点
void dfs(const vector<vector<int>>& rooms, int key, vector<bool>& visited) {
// 这里 没有终止条件,而是在 处理下一层节点的时候来判断
vector<int> keys = rooms[key];
for (int key : keys) {
if (visited[key] == false) { // 处理下一层节点,判断是否要进行递归
visited[key] = true;
dfs(rooms, key, visited);
}
}
}
// 写法一:处理当前访问的节点
class Solution {
private:
void dfs(const vector<vector<int>>& rooms, int key, vector<bool>& visited) {
if (visited[key]) {
return;
}
visited[key] = true;
vector<int> keys = rooms[key];
for (int key : keys) {
// 深度优先搜索遍历
dfs(rooms, key, visited);
}
}
public:
bool canVisitAllRooms(vector<vector<int>>& rooms) {
vector<bool> visited(rooms.size(), false);
dfs(rooms, 0, visited);
//检查是否都访问到了
for (int i : visited) {
if (i == false) return false;
}
return true;
}
};
写法二:处理下一个要访问的节点
class Solution {
private:
void dfs(const vector<vector<int>>& rooms, int key, vector<bool>& visited) {
vector<int> keys = rooms[key];
for (int key : keys) {
if (visited[key] == false) {
visited[key] = true;
dfs(rooms, key, visited);
}
}
}
public:
bool canVisitAllRooms(vector<vector<int>>& rooms) {
vector<bool> visited(rooms.size(), false);
visited[0] = true; // 0 节点是出发节点,一定被访问过
dfs(rooms, 0, visited);
//检查是否都访问到了
for (int i : visited) {
if (i == false) return false;
}
return true;
}
};
class Solution {
bool bfs(const vector<vector<int>>& rooms) {
vector<int> visited(rooms.size(), 0); // 标记房间是否被访问过
visited[0] = 1; // 0 号房间开始
queue<int> que;
que.push(0); // 0 号房间开始
// 广度优先搜索的过程
while (!que.empty()) {
int key = que.front(); que.pop();
vector<int> keys = rooms[key];
for (int key : keys) {
if (!visited[key]) {
que.push(key);
visited[key] = 1;
}
}
}
// 检查房间是不是都遍历过了
for (int i : visited) {
if (i == 0) return false;
}
return true;
}
public:
bool canVisitAllRooms(vector<vector<int>>& rooms) {
return bfs(rooms);
}
};
class Solution {
private void dfs(int key, List<List<Integer>> rooms, List<Boolean> visited) {
if (visited.get(key)) {
return;
}
visited.set(key, true);
for (int k : rooms.get(key)) {
// 深度优先搜索遍历
dfs(k, rooms, visited);
}
}
public boolean canVisitAllRooms(List<List<Integer>> rooms) {
List<Boolean> visited = new ArrayList<Boolean>(){{
for(int i = 0 ; i < rooms.size(); i++){
add(false);
}
}};
dfs(0, rooms, visited);
//检查是否都访问到了
for (boolean flag : visited) {
if (!flag) {
return false;
}
}
return true;
}
}
// 广度优先搜索
class Solution {
public boolean canVisitAllRooms(List<List<Integer>> rooms) {
boolean[] visited = new boolean[rooms.size()]; // 用一个 visited 数据记录房间是否被访问
visited[0] = true;
Queue<Integer> queue = new ArrayDeque<>();
queue.add(0); // 第 0 个房间标记为已访问
while (!queue.isEmpty()) {
int curKey = queue.poll();
for (int key: rooms.get(curKey)) {
if (visited[key]) continue;
visited[key] = true;
queue.add(key);
}
}
for (boolean key: visited)
if (!key) return false;
return true;
}
}
// 广度优先遍历(时间优化)
class Solution {
public boolean canVisitAllRooms(List<List<Integer>> rooms) {
int count = 1; // 用来记录可以被访问的房间数目,因为初始状态下 0 号房间可以被访问,所以置为 1
boolean[] visited = new boolean[rooms.size()]; // 用一个 visited 数据记录房间是否被访问
visited[0] = true; // 第 0 个房间标记为已访问
Queue<Integer> queue = new ArrayDeque<>();
queue.add(0);
while (!queue.isEmpty()) {
int curKey = queue.poll();
for (int key: rooms.get(curKey)) {
if (visited[key]) continue;
++count; // 每访问一个访问房间就让 count 加 1
visited[key] = true;
queue.add(key);
}
}
return count == rooms.size(); // 如果 count 等于房间数目,表示能进入所有房间,反之不能
}
}
# 深度搜索优先
class Solution:
def dfs(self, key: int, rooms: List[List[int]] , visited : List[bool] ) :
if visited[key] :
return
visited[key] = True
keys = rooms[key]
for i in range(len(keys)) :
# 深度优先搜索遍历
self.dfs(keys[i], rooms, visited)
def canVisitAllRooms(self, rooms: List[List[int]]) -> bool:
visited = [False for i in range(len(rooms))]
self.dfs(0, rooms, visited)
# 检查是否都访问到了
for i in range(len(visited)):
if not visited[i] :
return False
return True
# 广度搜索优先
class Solution:
def canVisitAllRooms(self, rooms: List[List[int]]) -> bool:
visited = [False] * len(rooms)
self.bfs(rooms, 0, visited)
for room in visited:
if room == False:
return False
return True
def bfs(self, rooms, index, visited):
q = collections.deque()
q.append(index)
visited[0] = True
while len(q) != 0:
index = q.popleft()
for nextIndex in rooms[index]:
if visited[nextIndex] == False:
q.append(nextIndex)
visited[nextIndex] = True
func dfs(key int, rooms [][]int, visited []bool ) {
if visited[key] {
return;
}
visited[key] = true
keys := rooms[key]
for _ , key := range keys {
// 深度优先搜索遍历
dfs(key, rooms, visited);
}
}
func canVisitAllRooms(rooms [][]int) bool {
visited := make([]bool, len(rooms));
dfs(0, rooms, visited);
//检查是否都访问到了
for i := 0; i < len(visited); i++ {
if !visited[i] {
return false;
}
}
return true;
}
//DFS
var canVisitAllRooms = function(rooms) {
const dfs = (key, rooms, visited) => {
if(visited[key]) return;
visited[key] = 1;
for(let k of rooms[key]){
// 深度优先搜索遍历
dfs(k, rooms, visited);
}
}
const visited = new Array(rooms.length).fill(false);
dfs(0, rooms, visited);
//检查是否都访问到了
for (let i of visited) {
if (!i) {
return false;
}
}
return true;
};
//BFS
var canVisitAllRooms = function(rooms) {
const bfs = rooms => {
const visited = new Array(rooms.length).fill(0); // 标记房间是否被访问过
visited[0] = 1; // 0 号房间开始
const queue = []; //js数组作为队列使用
queue.push(0); // 0 号房间开始
// 广度优先搜索的过程
while(queue.length !== 0){
let key = queue[0];
queue.shift();
for(let k of rooms[key]){
if(!visited[k]){
queue.push(k);
visited[k] = 1;
}
}
}
// 检查房间是不是都遍历过了
for(let i of visited){
if(i === 0) return false;
}
return true;
}
return bfs(rooms);
};
// BFS
// rooms :就是一个链接表 表示的有向图
// 转换问题就是,一次遍历从 0开始 能不能 把所有的节点访问了,实质问题就是一个
// 层序遍历
function canVisitAllRooms(rooms: number[][]): boolean {
const n = rooms.length;
// cnt[i] 代表节点 i 的访问顺序, cnt[i] = 0, 代表没被访问过
let cnt = new Array(n).fill(0);
let queue = [0];
cnt[0]++;
while (queue.length > 0) {
const from = queue.shift();
for (let i = 0; i < rooms[from].length; i++) {
const to = rooms[from][i];
if (cnt[to] == 0) {
queue.push(to);
cnt[to]++;
}
}
}
// 只要其中有一个节点 没被访问过,那么就返回 false
return cnt.every((item) => item != 0);
}

